 |
|
|
Site Navigation
Projects & Information
»General Information»Wind turbine Projects »The F&P Smartdrive »Electronic projects »Microcontroller projects »Miscellaneous Kits & Parts
»Basicly Natural Pty Ltd»PVC & Aluminium blades »Scale model farm windmills »Price Watch Discussion Forums
Handy Links
»Wind»Solar »Electric Vehicles »Electronics »Micro Controllers »General Interrest About TheBackShed Getting Started Privacy Policy Understanding Swept Area
 A look at how the swept area, and therefore the power, of a turbine changes with diameter. |
There is a limit to the amount of power we can extract from the wind.
Say we wanted to calculate the power at a wind speed of 5ms ( 18kmh, an average windy day ), we use
How does wind speed affect the power? A great deal! If we double our wind speed to 10ms ( 36kmh ), we end up with 1920watts! That is why its important to know how much wind speed you have, and why windmills are put on tall towers, to get as many extra ms as possible. Getting back to our average windy day wind speed, the 240 watts is how much power is in that column of moving air, but its not how much we can extract from it to do work.
There is a limit to how much energy we can extract from a column of moving air, called Betz. http://en.wikipedia.org/wiki/Betz'_law And Betz tells us we can extract no more than 59% of the energy of the moving column of air. There is a point where the air will just go around instead of through, adding extra widgets to the turbine, funnels, etc, wont help, the air will just find it easier to go around. The maximum efficiency of a turbine can not exceed 59%. In reality, the true power we can extract is much less than the Betz limit. A multi blade farm windmill has a typical efficiency of 15%, and modern large scale wind turbines are closer to 40% efficient. So adding to our formula
So if we attach a shaft to our 2 meter wind turbine, we would expect to extract about 96 watts of shaft power from the 5ms wind. Next we use our shaft power to drive a alternator/generator, and again, we will get out less than we put in. A good alternator is somewhere between 70% to 90% efficient, so for the sake of this example, we'll use a 80% efficient alternator. 96 watts shaft power will convert to about 77 watts of electrical power. So our 2 meter turbine, in a 5ms wind, could be expected to make 77 watts of electrical power. Adding to our formula again we get
Turbine diameter and wind speed have a dramatic effect on the electrical power we get extract. If we increase the turbines diameter to 3 meters, we get a turbine area of 7 meters, more than double the original turbines area. Punch the figures in and we get 535watts wind power, 214watts shaft power, and 171watts electrical power. What about wind speed? Back to our original 2 meter turbine, double the wind speed to 10ms, gives us 1923watts wind power, 769watts shaft power, and 615 watts electrical power. That's why its important to have the biggest turbine you can manage, and the best wind. A 1.5 meter turbine mounted on the roof or in the back yard is going to make very little power compared to a 3 meter turbine on a 10 meter mast, its all in the maths. Further Reading... |
||
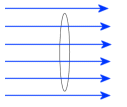 Imagine a circular column of moving air, or wind, 2 meters across. We can calculate how much power is in that moving column of wind with the following
Imagine a circular column of moving air, or wind, 2 meters across. We can calculate how much power is in that moving column of wind with the following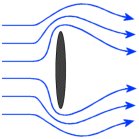 Air is a compressible fluid. If we face a 2 meter diameter disc into the wind, there will be some force against the disc from the wind, but not the full 240watts worth. The wind will go around the disc, and most of the power goes with it.
Air is a compressible fluid. If we face a 2 meter diameter disc into the wind, there will be some force against the disc from the wind, but not the full 240watts worth. The wind will go around the disc, and most of the power goes with it. 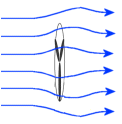 What about a turbine? A turbine extracts much more energy from the column of moving air than the disc did, because the air is moving through the turbine, not around it. But some air will still go around. How much air goes around depends on many factors, like turbine design and loading.
What about a turbine? A turbine extracts much more energy from the column of moving air than the disc did, because the air is moving through the turbine, not around it. But some air will still go around. How much air goes around depends on many factors, like turbine design and loading.