
|

|
Forum Index : Microcontroller and PC projects : The Great Colour Maximite 2 Octahedron Prize Challenge
| Author | Message | ||||
| PeteCotton Guru Joined: 13/08/2020 Location: CanadaPosts: 604 |
Very nice. I really like the way you're calculating the smallest box to erase! Very good idea. |
||||
| PeteCotton Guru Joined: 13/08/2020 Location: CanadaPosts: 604 |
I would still be over the moon with that number. I'm at 1043ms (on a 480mhz), so you have well and truely trounced my time  Brilliant work. Brilliant work. |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
Thanks! It cost me a few ms with RC14, but it allowed mucking with the octahedron (and icosahedron) geometry without needing to re-figure out the erasing box. I haven't tested it speedwise with the new release candidates. MIN and MAX functions are remarkably useful. They're fast and can replace statements like: IF newval < bestval THEN bestval = newval -- change to -- bestval = MIN(newval,bestval) Visit Vegipete's *Mite Library for cool programs. |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
Don't be too amazed yet. Peter might just disqualify me for 'cheating' because of some of the loop unrolling I've done. Optimizing for speed and optimizing for size are usually opposite. I've gone deep into the fast and long end of things. For example, my iteration loop contains 69 lines of code/statements. ==== Btw, could you check which iteration you are printing the vertex coordinates for? Are you saving them at the top of the loop or the bottom? Visit Vegipete's *Mite Library for cool programs. |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
What vigipete did is amazing. My time after adding the absolute angle calculation jumped to 1218.85ms. I'm using the RC19 firmware. Now, the end octahedron position is the same as the beginning. My main loop has only 22 lines and even with fewer lines compared to your code loop I'm just near to the double of your execution time, and I'm running it on a 480MHz CMM2. [EDIT: I forgot that I have more than one command per line] Congratulations  Edited 2020-11-15 06:46 by LeoNicolas |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
That's about 200 ms longer? Hmm. Here's my rotation matrix generation code: ' Note: OPTION ANGLE DEGREES cx = cos(2*iter) : sx = sin(2*iter) ' GRRR - rule change cy = cos(1*iter) : sy = sin(1*iter) ' must recalc rotation matrix cz = cos(.5*iter) : sz = sin(.5*iter) ' each iteration trot(0,0) = cz * cy trot(1,0) = sz * cy trot(2,0) = sy trot(0,1) = cz * sx * sy - sz * cx trot(1,1) = cz * cx + sz * sx * sy trot(2,1) = - sx * cy trot(0,2) = - cz * cx * sy - sz * sx trot(1,2) = cz * sx - sz * cx * sy trot(2,2) = cx * cy Since it is rotation only, I don't need to use homogeneous coordinates so a 3x3 matrix is plenty. Visit Vegipete's *Mite Library for cool programs. |
||||
| PeteCotton Guru Joined: 13/08/2020 Location: CanadaPosts: 604 |
It's still an amazing feat. I suspect even without the loop unrolling you would still have me beat hands down. As for the iteration for the vertex co-ordinates, I'm not sure i understand the question? I start at 0 and run to 719. I take the vertex calcs for iterain #649 (i.e. the 650th based on the zero based loop) - after I have applied the transform. I'm not sure if that's what you are asking? |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
I'm just wondering why my iteration 649 equals your iteration 650. Visit Vegipete's *Mite Library for cool programs. |
||||
| PeteCotton Guru Joined: 13/08/2020 Location: CanadaPosts: 604 |
Ah! you are quite right. I switch so many things around when optomising my code that I often lose track of the simple stuff. When I look at my code I am indeed copying them over before I save the calculation. here's the real 650th ones. 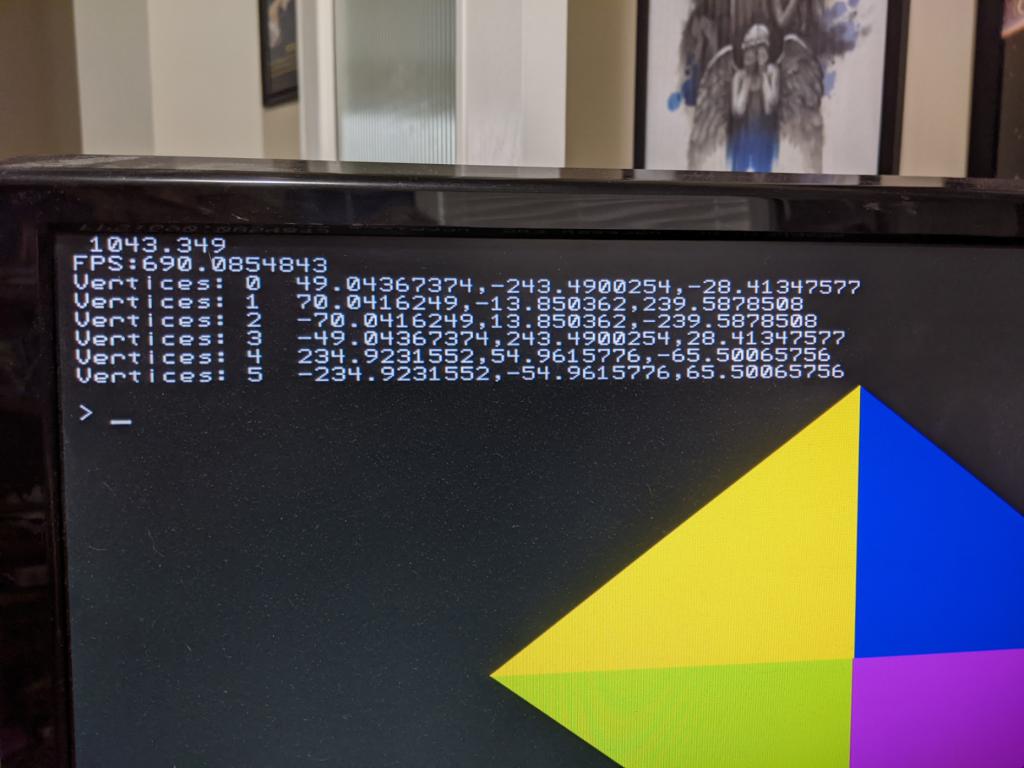 |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
Great stuff. We match to every decimal place, although not in sign. Vertex coordinates at iteration 650: -49.04367374 -243.4900254 -28.41347577 70.0416249 13.850362 -239.5878508 -70.0416249 -13.850362 239.5878508 49.04367374 243.4900254 28.41347577 -234.9231552 54.9615776 -65.50065756 234.9231552 -54.9615776 65.50065756 Looks like our x-axis handedness is opposite. I can live with that. Visit Vegipete's *Mite Library for cool programs. |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
The same values here. I've fixed an issue and now my time is 1057ms. I'm using matrix multiplication, maybe using direct calculation will be fast. I'll try it. .jpg) Edited 2020-11-15 08:39 by LeoNicolas |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
vigipete, the credits for this optimization go to you. I reached 1001.97 ms PS: I'm not counting the time to print the 650th data. sub pv(vrt) tt=timer ... print the vertices timer=tt end sub 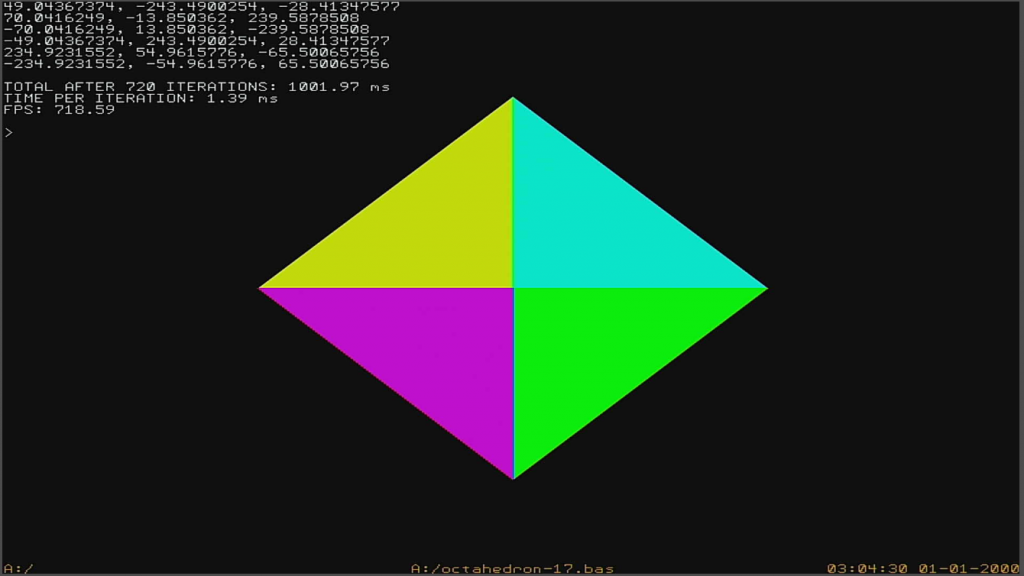 Edited 2020-11-15 09:10 by LeoNicolas |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
Finally, I've got an execution time below 1s  Total execution time: 968.25 ms  Edited 2020-11-16 16:02 by LeoNicolas |
||||
| PeteCotton Guru Joined: 13/08/2020 Location: CanadaPosts: 604 |
Just a quick update on this. I've got an efficient algorithm for mapping triangles working well. It turned out to be trickier than I thought due to all of the combinations of source image points and destination points, flipped images etc. But it handles them all well now. Basically throw any 3 destination points and any 3 source points (and the source graphics page number) and it will map it correctly. The best method I could come up with was to split the triangle in two and draw it as a flat bottomed triangle on top of a flat topped triangle. This allows me to walk down the outside edges of the top triangle, and then walk down the outside edges of the bottom triangle. In the image below I have drawn in this extra 4th point and the split line between the two triangles. So the top triangle is P1-P4-P2 and the bottom one is P2-P4-P3.  I had hoped to be able to use this to create rectangles by splitting the rectangles in to two triangles (see below), however it distorts the mapped image. (in the picture below the right hand triangle takes up more physical on screen pixels than the left hand one - yet they are mapping the same number of pixels from the source image). But not to worry, now that I have the triangle code working, it's a simple task to alter it to work with a four sided shape. I will get that working in the next few days. 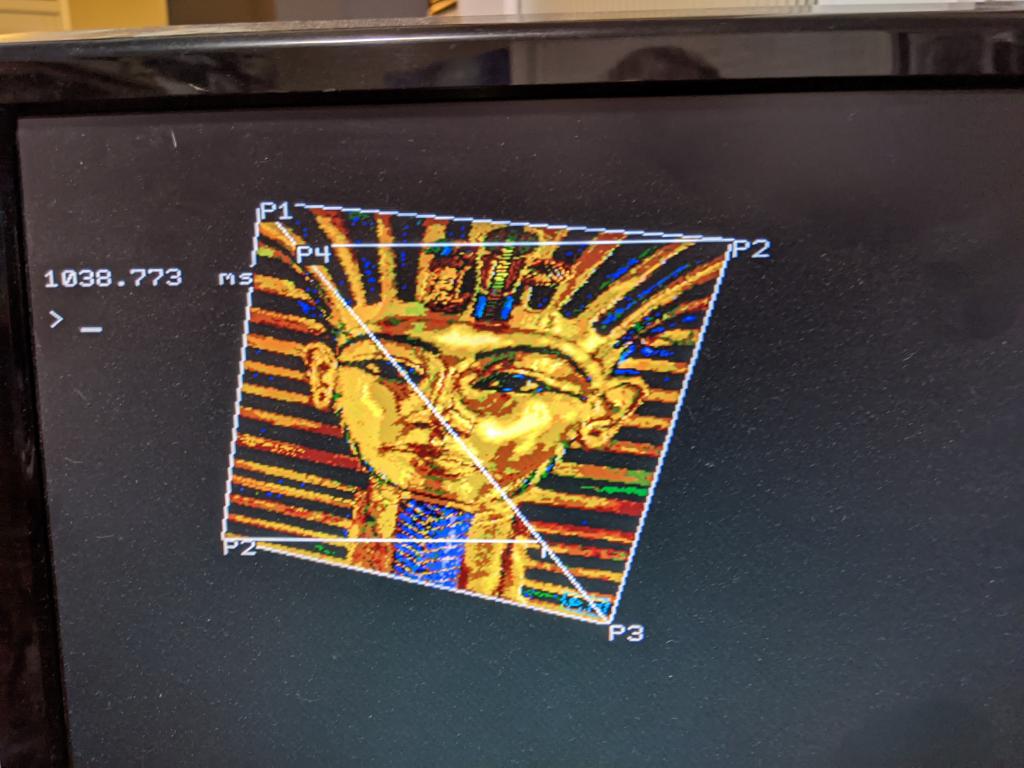 After I have the rectangle working I will post the code for both functions here. Maybe you guys could improve upon it? Speed it up? Find bugs etc. The algorithm itself is pretty simple. Edited 2020-11-18 10:55 by PeteCotton |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
Pete, this is very cool  I thinking that this algorithm can help me with the polygon clipping. The result of clipping a triangle can be a rectangle or a pentagon and to keep the triangle mesh coherence it's necessary to divide the resulting polygon into new triangles. |
||||
| PeteCotton Guru Joined: 13/08/2020 Location: CanadaPosts: 604 |
It occurs to me that it is currently Friday the 20th Nov for our antipodean mates. (The closing date of the competition). So here is my code for what it is worth. I suspect the others have me beat hands down, but it was a lot of fun, and thanks to everyone involved for the comaraderie. On the off chance that I do win, I will quite happily pass on the prize and see it go to a worthy soul. I just appreciated the opportunity to compete. RotatePeteC.zip timer=0 option explicit option base 0 option default none option angle degrees mode 1,8 const VERTS=5 ' Max of zero based array. So this is for 6 vertices and 8 planes const PLANES=7 const RX=2 ' X Rotation const RY=1 ' Y Rotation const RZ=0.5 ' Z Rotation dim float p1,p2,p3,x1,x2,x3,y1,y2,y3,z1,z2,z3,dx1,dx2,dy1,dy2 dim float snx,sny,snz,csx,csy,csz,x,y,z, finalTime,fps,nx,ny,nz,v1,v2,v3, opv dim integer k,v,n,t dim float dnx(VERTS) ' Stores the translated X,Y,Z co-ords of each node/vertex dim float dny(VERTS) dim float dnz(VERTS) dim integer cl(PLANES) ' The colour of each side/plane cl(0)=rgb(0,255,255) cl(1)=rgb(255,128,0) cl(2)=rgb(128,255,0) cl(3)=rgb(128,0,255) cl(4)=rgb(255,0,0) cl(5)=rgb(0,255,0) cl(6)=rgb(0,0,255) cl(7)=rgb(255,255,0) ' Vertex data is stored in 2 dimensional array where the 2nd dimension defines x, y or z dim float vx(VERTS) ' Store 6 vertex points of x, y and z co-ordinates dim float vy(VERTS) dim float vz(VERTS) vx(0)=0:vy(0)=250:vz(0)=0 vx(1)=250:vy(1)=0:vz(1)=0 vx(2)=-250:vy(2)=0:vz(2)=0 vx(3)=0:vy(3)=-250:vz(3)=0 vx(4)=0:vy(4)=0:vz(4)=250 vx(5)=0:vy(5)=0:vz(5)=-250 dim float pn(PLANES,3) ' Planes are made up of 3 or 4 vertexes pn(0,0)=0:pn(0,1)=5:pn(0,2)=2 pn(1,0)=0:pn(1,1)=1:pn(1,2)=5 pn(2,0)=0:pn(2,1)=2:pn(2,2)=4 pn(3,0)=0:pn(3,1)=4:pn(3,2)=1 pn(4,0)=3:pn(4,1)=2:pn(4,2)=5 pn(5,0)=3:pn(5,1)=5:pn(5,2)=1 pn(6,0)=3:pn(6,1)=1:pn(6,2)=4 pn(7,0)=3:pn(7,1)=4:pn(7,2)=2 ' Pre-process the object and see if any planes are parallel but opposite direction of any ' other plane. If it is, then we can deduce whether the second plane is visible from the ' visibilty of the opposing plane ' This masively reduces the calculation time for all 3d primitives with an even number of sides ' greater than or equal to 6. So cubes, walls, doors, cylinders, poly-spheres all benefit greatly ' from this pre-calc. It' less effective on complex shapes, but does not make them any slower ' So it's always worth doing. ' Note: this code is not specific to the octohedron - it works on any shape dim integer op(PLANES) ' Oposite plane number (if any) dim integer rn(PLANES) ' Has this plane been rendered (reset to zero evert new frame) ' Calculate the normal vector (as cross product) for each plane in the object ' Store these 3d normal vectors in crx(),cry(),crz() arrays dim float crx(PLANES) dim float cry(PLANES) dim float crz(PLANES) for n=0 to PLANES p1=pn(n,0):p2=pn(n,1):p3=pn(n,2) x1=vx(p1):y1=vy(p1):z1=vz(p1):x2=vx(p2):y2=vy(p2):z2=vz(p2) x3=vx(p3):y3=vy(p3):z3=vz(p3) crz(n)=(x1-x2)*(y1-y3)-(y1-y2)*(x1-x3) crx(n)=(z1-z2)*(y1-y3)-(y1-y2)*(z1-z3) cry(n)=(x1-x2)*(z1-z3)-(z1-z2)*(x1-x3) next n 'Look at each plane's normal vector and see if any of the preceeding planes are exactly opposite for n=1 to PLANES op(n)=n ' By default, if the value is the same as the plane number, then it will be calculated for v=0 to n-1 if crx(n)=-crx(v) and cry(n)=-cry(v) and crz(n)=-crz(v) then op(n)=v ' Plane v is the opposite plane of n exit for endif next v next n ' Preprocess vertexes and see if any are mirrored ' ov(x) holds the index of the opposite vertex + 1 (so that we can use zero to represent no mirror) dim integer ov(VERTS) dim float opx(VERTS),opy(VERTS),opz(VERTS) ' used to store the opposite vertexes values each loop for n=1 to VERTS ov(n)=0 for v=0 to n-1 if vx(v)=-vx(n) and vy(v)=-vy(n) and vz(v)=-vz(n) then ov(n)=v+1 exit for endif next v next n ' The above code produces the following values for my octohedron, but it will be different ' for any other 3D shape 'op(0)=0 'op(1)=1 'op(2)=2 'op(3)=3 'op(4)=3 ' Opposite to plane 3 'op(5)=2 ' Opposite to plane 2 'op(6)=0 ' Opposite to plane 0 'op(7)=1 ' Opposite to plane 1 'ov(0)=0 'ov(1)=0 'ov(2)=2 'opposite to vertex 1 'ov(3)=1 'opposite to vertex 0 'ov(4)=0 'ov(5)=5 'opposite to vertex 4 'page write 1 cls 'Main loop dim float ax,ay,az for k=0 to 719 inc ax,rx: inc ay,ry: inc az,rz snz=sin(az):csz=cos(az):sny=sin(ay):csy=cos(ay):snx=sin(ax):csx=cos(ax) for n=0 to VERTS ' Rotate vertices if ov(n) then ' there is a mirror for this vertex - invert the x,y and z and bob's yer uncle opv=ov(n)-1 ' Apply real world transform for perspective v1=800/(1000-opz(opv)) dnx(n)=v1*opx(opv):dny(n)=v1*opy(opv) ' this is a mirror vertex else x=vx(n):y=vy(n):z=vz(n) nx=x*csz-y*snz:ny=y*csz+x*snz ' Rotate around z nz=z*csy-nx*sny:nx=nx*csy+z*sny ' Rotate around y z=nz:nz=z*csx+ny*snx:ny=ny*csx-z*snx ' Rotate around x opx(n)=-nx:opy(n)=-ny:opz(n)=-nz ' Record the rotated positions for mirrored vertices ' Apply real world transform for perspective '800 viewplane distance, 1000 object distance from viewer v1=800/(1000-nz):dnx(n)=nx*v1:dny(n)=ny*v1 endif next n box 192,94,416,413,0,0,0 math set 1,rn() ' if rn(x)=0 then that side has been rendered for v=0 to PLANES ' Draw faces if rn(op(v)) then ' we have not rendered the opposite side yet p1=pn(v,0):p2=pn(v,1):p3=pn(v,2) dx1=dnx(p1):dy1=dny(p1) if (dx1-dnx(p2))*(dy1-dny(p3))>(dy1-dny(p2))*(dx1-dnx(p3)) then ' Cross product triangle 400+dx1,300+dy1,400+dnx(p2),300+dny(p2),400+dnx(p3),300+dny(p3),cl(v),cl(v) rn(v)=0 ' Remember that this face was rendered end if endif next v ' page copy 1,0,i next k 'Output final stats finalTime= timer print finalTime fps=(720/finalTime)*1000 print "FPS:" + str$(fps) ' Calculate rotations around center of object (i.e. spin) snz=sin(649*RZ):csz=cos(649*RZ):sny=sin(649*RY):csy=cos(649*RY):snx=sin(649*RX):csx=cos(649*RX) for n=0 to VERTS ' Rotate vertices x=vx(n):y=vy(n):z=vz(n) nx=x*csz-y*snz:ny=y*csz+x*snz ' Rotate around z nz=z*csy-nx*sny:nx=nx*csy+z*sny ' Rotate around y z=nz:nz=z*csx+ny*snx:ny=ny*csx-z*snx ' Rotate around x print "Vertices: " + str$(n) + " " + str$(nx) + "," + str$(ny) + "," + str$(nz) next n 'Page copy 1,0 |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
Pete, thank you for sharing your code. Due to the bug with the INC command, my code only runs correctly until the RC20. octahedron-20.bas.zip This is my code: option explicit option keyboard repeat 400,40 option base 0 option default float option angle degrees timer=0 mode 1,8 ' Aux variables dim f,i,v, x(2),y(2),z,vi(2),vo(2),tt ' Object data - distance X,Y,Z - Viewplane distance - Vertices and Faces arrays size const dx=400,dy=300,dz=1000,vp=800,vs=5,fs=7 ' Projection matrix dim px(vs),py(vs) ' Vertices dim vt(2,vs)=(0,250,0, 250,0,0, -250,0,0, 0,-250,0, 0,0,250, 0,0,-250) ' Faces dim f1(fs)=(5,5,5,5,4,4,4,4) dim f2(fs)=(2,3,1,0,3,1,0,2) dim f3(fs)=(3,1,0,2,2,3,1,0) ' Faces colors dim c(fs)=(rgb(yellow),rgb(cyan),rgb(green),rgb(magenta),rgb(red),rgb(blue),rgb(white),rgb(&H40,&H40,&H40)) ' Rotation - Angles X,Y,Z - Rotation matrix const ix=2,iy=1,iz=0.5 dim ax,ay,az, cx,sx, cy,sy, cz,sz, r(2,2) ' Main loop cls for i=1 to 720 box 192,92,416,416,,0,0 inc ax,ix:inc ay,iy:inc az,iz cx=cos(ax):sx=sin(ax) cy=cos(ay):sy=sin(ay) cz=cos(az):sz=sin(az) r(0,0)=cy*cz:r(0,1)=sx*sy*cz-sz*cx:r(0,2)=-sy*cx*cz-sx*sz r(1,0)=cy*sz:r(1,1)=cx*cz+sx*sy*sz:r(1,2)=sx*cz-sz*cx*sy r(2,0)=sy:r(2,1)=-sx*cy:r(2,2)=cx*cy for v=0 to vs math slice vt(),,v,vi() math v_mult r(),vi(),vo() z=vp/(dz+vo(2)):px(v)=vo(0)*z+dx:py(v)=vo(1)*z+dy if i=650 then pv(vo()) end if next for f=0 to fs v=f1(f):x(0)=px(v):y(0)=py(v) v=f2(f):x(1)=px(v):y(1)=py(v) v=f3(f):x(2)=px(v):y(2)=py(v) math v_cross x(),y(),vo() if math(sum vo())>0 then polygon 3,x(),y(),c(f),c(f) end if next next tt=timer ' Execution statistics page write 0 print "TOTAL AFTER "+str$(i-1)+" ITERATIONS: "+str$(tt,0,2)+" ms" print "TIME PER ITERATION: "+str$(tt/720,0,2)+" ms" print "FPS: "+str$(1000/(tt/720),0,2) sub pv(vrt()) tt=timer math v_print vrt() timer=tt end sub Edited 2020-11-20 09:48 by LeoNicolas |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
Yes indeed, show and tell time. My version listed here runs nicely on RC18. I haven't tested any higher ones. So there are still hex constants in the code. Also, the fixed size erase box is a few milliseconds faster than the dynamically sized erase box. The speed boost that might be cheating? I elected to encode the face data in the program not in data statements but as program statements. Thus there are 8 largely identical IF statements, one for each face, instead of an inner loop iterating over the faces. This was fast because it dramatically reduced access to (multi-)dimensional arrays. Something I didn't get around to testing was whether adding the projection step to the rotation matrix would shave some more time. A big thank you to others who help motivate the quest for speed. It's been fun! I look forward to dissecting the other entries to learn. ' Octaspin ' vegipete, November, 2020 ' optimized for 5.05.06RC18 mode 1,8 cls timer = 0 '====================================== option angle degrees d = 800 ' distance to view plane rho = 1000 ' distance to object (center) cenx = MM.HRES/2 ceny = MM.VRES/2 restore octashape ' read in 6 vertices dim v0(2) : read v0(0) : read v0(1) : read v0(2) dim v1(2) : read v1(0) : read v1(1) : read v1(2) dim v2(2) : read v2(0) : read v2(1) : read v2(2) dim v3(2) : read v3(0) : read v3(1) : read v3(2) dim v4(2) : read v4(0) : read v4(1) : read v4(2) dim v5(2) : read v5(0) : read v5(1) : read v5(2) dim vt0(2) ' temp vectors dim vt1(2) dim vt2(2) dim vt3(2) dim vt4(2) dim vt5(2) dim vs0(2) ' save vectors - for iteration 650 dim vs1(2) dim vs2(2) dim vs3(2) dim vs4(2) dim vs5(2) dim trot(2,2) ' total rotation matrix ' draw iteration 0 ze=rho-v0(&h2) : x0=-d*v0(&h0)/ze : y0=d*v0(&h1)/ze ' project 6 points ze=rho-v1(&h2) : x1=-d*v1(&h0)/ze : y1=d*v1(&h1)/ze ze=rho-v2(&h2) : x2=-d*v2(&h0)/ze : y2=d*v2(&h1)/ze ze=rho-v3(&h2) : x3=-d*v3(&h0)/ze : y3=d*v3(&h1)/ze ze=rho-v4(&h2) : x4=-d*v4(&h0)/ze : y4=d*v4(&h1)/ze ze=rho-v5(&h2) : x5=-d*v5(&h0)/ze : y5=d*v5(&h1)/ze if (x4-x2)*(y4-y3)<(x4-x3)*(y4-y2) then ' face 0: 4,2,3 triangle x4+cenx,y4+ceny,x2+cenx,y2+ceny,x3+cenx,y3+ceny,&hFF0000,&hFF0000 endif if (x4-x3)*(y4-y1)<(x4-x1)*(y4-y3) then ' face 1: 4,3,1 triangle x4+cenx,y4+ceny,x3+cenx,y3+ceny,x1+cenx,y1+ceny,&h00FF00,&h00FF00 endif if (x4-x1)*(y4-y0)<(x4-x0)*(y4-y1) then ' face 2: 4,1,0 triangle x4+cenx,y4+ceny,x1+cenx,y1+ceny,x0+cenx,y0+ceny,&h0000FF,&h0000FF endif if (x4-x0)*(y4-y2)<(x4-x2)*(y4-y0) then ' face 3: 4,0,2 triangle x4+cenx,y4+ceny,x0+cenx,y0+ceny,x2+cenx,y2+ceny,&hFFFF00,&hFFFF00 endif if (x5-x3)*(y5-y2)<(x5-x2)*(y5-y3) then ' face 4: 5,3,2 triangle x5+cenx,y5+ceny,x3+cenx,y3+ceny,x2+cenx,y2+ceny,&hFF00FF,&hFF00FF endif if (x5-x1)*(y5-y3)<(x5-x3)*(y5-y1) then ' face 5: 5,1,3 triangle x5+cenx,y5+ceny,x1+cenx,y1+ceny,x3+cenx,y3+ceny,&h00FFFF,&h00FFFF endif if (x5-x0)*(y5-y1)<(x5-x1)*(y5-y0) then ' face 6: 5,0,1 triangle x5+cenx,y5+ceny,x0+cenx,y0+ceny,x1+cenx,y1+ceny,&hFFFFFF,&hFFFFFF endif if (x5-x2)*(y5-y0)<(x5-x0)*(y5-y2) then ' face 7: 5,2,0 triangle x5+cenx,y5+ceny,x2+cenx,y2+ceny,x0+cenx,y0+ceny,&h404040,&h404040 endif for iter = 1 to 720 cx = cos(2*iter) : sx = sin(2*iter) ' GRRR - rule change cy = cos(1*iter) : sy = sin(1*iter) ' must recalc rotation matrix cz = cos(.5*iter) : sz = sin(.5*iter) ' each iteration trot(0,0) = cz * cy trot(1,0) = sz * cy trot(2,0) = sy trot(0,1) = cz * sx * sy - sz * cx trot(1,1) = cz * cx + sz * sx * sy trot(2,1) = - sx * cy trot(0,2) = - cz * cx * sy - sz * sx trot(1,2) = cz * sx - sz * cx * sy trot(2,2) = cx * cy math v_mult trot(),v0(),vt0() ' rotate math v_mult trot(),v1(),vt1() ' 6 points math v_mult trot(),v2(),vt2() ' in math v_mult trot(),v3(),vt3() ' three math v_mult trot(),v4(),vt4() ' dimensions math v_mult trot(),v5(),vt5() ' bx = min(x0,x1,x2,x3,x4,x5)+cenx : bh = max(x0,x1,x2,x3,x4,x5)+cenx+&h2 ' calculate ' by = min(y0,y1,y2,y3,y4,y5)+ceny : bv = max(y0,y1,y2,y3,y4,y5)+ceny+&h2 ' erasing box ' box bx,by,bh-bx,bv-by,,&h0,&h0 ' erase previous image - dynamic size calc box 193,92,416,420,0,0,0 ' slightly faster than calculated box ze=rho-vt0(&h2) : x0=-d*vt0(&h0)/ze : y0=d*vt0(&h1)/ze ' project 6 points ze=rho-vt1(&h2) : x1=-d*vt1(&h0)/ze : y1=d*vt1(&h1)/ze ze=rho-vt2(&h2) : x2=-d*vt2(&h0)/ze : y2=d*vt2(&h1)/ze ze=rho-vt3(&h2) : x3=-d*vt3(&h0)/ze : y3=d*vt3(&h1)/ze ze=rho-vt4(&h2) : x4=-d*vt4(&h0)/ze : y4=d*vt4(&h1)/ze ze=rho-vt5(&h2) : x5=-d*vt5(&h0)/ze : y5=d*vt5(&h1)/ze if (x4-x2)*(y4-y3)<(x4-x3)*(y4-y2) then ' face 0: 4,2,3 triangle x4+cenx,y4+ceny,x2+cenx,y2+ceny,x3+cenx,y3+ceny,&hFF0000,&hFF0000 endif if (x4-x3)*(y4-y1)<(x4-x1)*(y4-y3) then ' face 1: 4,3,1 triangle x4+cenx,y4+ceny,x3+cenx,y3+ceny,x1+cenx,y1+ceny,&h00FF00,&h00FF00 endif if (x4-x1)*(y4-y0)<(x4-x0)*(y4-y1) then ' face 2: 4,1,0 triangle x4+cenx,y4+ceny,x1+cenx,y1+ceny,x0+cenx,y0+ceny,&h0000FF,&h0000FF endif if (x4-x0)*(y4-y2)<(x4-x2)*(y4-y0) then ' face 3: 4,0,2 triangle x4+cenx,y4+ceny,x0+cenx,y0+ceny,x2+cenx,y2+ceny,&hFFFF00,&hFFFF00 endif if (x5-x3)*(y5-y2)<(x5-x2)*(y5-y3) then ' face 4: 5,3,2 triangle x5+cenx,y5+ceny,x3+cenx,y3+ceny,x2+cenx,y2+ceny,&hFF00FF,&hFF00FF endif if (x5-x1)*(y5-y3)<(x5-x3)*(y5-y1) then ' face 5: 5,1,3 triangle x5+cenx,y5+ceny,x1+cenx,y1+ceny,x3+cenx,y3+ceny,&h00FFFF,&h00FFFF endif if (x5-x0)*(y5-y1)<(x5-x1)*(y5-y0) then ' face 6: 5,0,1 triangle x5+cenx,y5+ceny,x0+cenx,y0+ceny,x1+cenx,y1+ceny,&hFFFFFF,&hFFFFFF endif if (x5-x2)*(y5-y0)<(x5-x0)*(y5-y2) then ' face 7: 5,2,0 triangle x5+cenx,y5+ceny,x2+cenx,y2+ceny,x0+cenx,y0+ceny,&h404040,&h404040 endif if iter = 650 then SaveVerts ' print @(700,0) iter : do : loop until inkey$ <> "" ' uncomment for step by step next iter print timer ShowVerts end sub SaveVerts vs0(0) = vt0(0) : vs0(1) = vt0(1) : vs0(2) = vt0(2) vs1(0) = vt1(0) : vs1(1) = vt1(1) : vs1(2) = vt1(2) vs2(0) = vt2(0) : vs2(1) = vt2(1) : vs2(2) = vt2(2) vs3(0) = vt3(0) : vs3(1) = vt3(1) : vs3(2) = vt3(2) vs4(0) = vt4(0) : vs4(1) = vt4(1) : vs4(2) = vt4(2) vs5(0) = vt5(0) : vs5(1) = vt5(1) : vs5(2) = vt5(2) end sub sub ShowVerts print : print "Vertex coordinates at iteration 650:" print vs0(0), vs0(1), vs0(2) print vs1(0), vs1(1), vs1(2) print vs2(0), vs2(1), vs2(2) print vs3(0), vs3(1), vs3(2) print vs4(0), vs4(1), vs4(2) print vs5(0), vs5(1), vs5(2) end sub octashape: ' vertices data 0,250,0, 250,0,0, -250,0,0, 0,-250,0, 0,0,250, 0,0,-250 ' faces - unused data 4,2,3, 4,3,1, 4,1,0, 4,0,2, 5,3,2, 5,1,3, 5,0,1, 5,2,0 Visit Vegipete's *Mite Library for cool programs. |
||||
| LeoNicolas Guru Joined: 07/10/2020 Location: CanadaPosts: 562 |
Nice job Pete and Vegipete This challenge was super fun. The problem with performance accessing multidimensional arrays is very clear and this is why I have used three unidimensional arrays for the octahedron faces. For the vertices, the math slice command gave me a performance boost and I decided to keep them in a multidimensional array. Edited 2020-11-20 13:10 by LeoNicolas |
||||
| vegipete Guru Joined: 29/01/2013 Location: CanadaPosts: 1160 |
For more entertainment value, here is my program , modified to spin an icosahedron. My run time is 1517 ms. (RC18, 400 MHz Waveshare) So that is roughly 650 ms longer to process 12 corners instead of 6, and 20 faces instead of 8. This program shows a slight bug I report once before. If a program ends with font size other than 1 (my standard size is the default 1), the screen scrolls _UP_ a few pixels, based on the difference in font size. See line 316. The vertex and face data (sized to match the octahedron) I used is: icosashape: ' vertices 'data 12 data 0,132,213, 0,-132,213, 0,132,-213, 0,-132,-213 ' (0, 1, f) Where f = data 132,213,0, -132,213,0, 132,-213,0, -132,-213,0 ' (1, f, 0) (1 + v5) / 2 data 213,0,132, 213,0,-132, -213,0,132, -213,0,-132 ' ( f, 0, 1) golden ratio 1.618 ' faces 'data 20 data 1, 6, 8, 1, 8, 0, 1, 0,10, 1,10, 7 ' vertices for data 1, 7, 6, 6, 7, 3, 6, 3, 9, 6, 9, 8 ' each face in data 8, 9, 4, 8, 4, 0, 0, 4, 5, 0, 5,10 ' counter-clockwise data 10, 5,11, 10,11, 7, 7,11, 3, 3,11, 2 ' order data 2,11, 5, 2, 5, 4, 2, 4, 9, 2, 9, 3 ' Icosaspin ' vegipete, November, 2020 ' optimized for 5.05.06RC18 mode 1,8 cls timer = 0 '====================================== option angle degrees d = 800 ' distance to view plane rho = 1000 ' distance to object (center) cenx = MM.HRES/2 ceny = MM.VRES/2 restore icosashape ' read in 12 vertices dim v0(2) : read v0(0) : read v0(1) : read v0(2) dim v1(2) : read v1(0) : read v1(1) : read v1(2) dim v2(2) : read v2(0) : read v2(1) : read v2(2) dim v3(2) : read v3(0) : read v3(1) : read v3(2) dim v4(2) : read v4(0) : read v4(1) : read v4(2) dim v5(2) : read v5(0) : read v5(1) : read v5(2) dim v6(2) : read v6(0) : read v6(1) : read v6(2) dim v7(2) : read v7(0) : read v7(1) : read v7(2) dim v8(2) : read v8(0) : read v8(1) : read v8(2) dim v9(2) : read v9(0) : read v9(1) : read v9(2) dim v10(2) : read v10(0) : read v10(1) : read v10(2) dim v11(2) : read v11(0) : read v11(1) : read v11(2) dim vt0(2) ' temp vectors dim vt1(2) dim vt2(2) dim vt3(2) dim vt4(2) dim vt5(2) dim vt6(2) dim vt7(2) dim vt8(2) dim vt9(2) dim vt10(2) dim vt11(2) dim vs0(2) ' save vectors - for iteration 650 dim vs1(2) dim vs2(2) dim vs3(2) dim vs4(2) dim vs5(2) dim vs6(2) dim vs7(2) dim vs8(2) dim vs9(2) dim vs10(2) dim vs11(2) dim trot(2,2) ' total rotation matrix ' draw iteration 0 ze=rho- v0(2) : x0=-d* v0(0)/ze : y0=d* v0(1)/ze ' project 12 points ze=rho- v1(2) : x1=-d* v1(0)/ze : y1=d* v1(1)/ze ze=rho- v2(2) : x2=-d* v2(0)/ze : y2=d* v2(1)/ze ze=rho- v3(2) : x3=-d* v3(0)/ze : y3=d* v3(1)/ze ze=rho- v4(2) : x4=-d* v4(0)/ze : y4=d* v4(1)/ze ze=rho- v5(2) : x5=-d* v5(0)/ze : y5=d* v5(1)/ze ze=rho- v6(2) : x6=-d* v6(0)/ze : y6=d* v6(1)/ze ze=rho- v7(2) : x7=-d* v7(0)/ze : y7=d* v7(1)/ze ze=rho- v8(2) : x8=-d* v8(0)/ze : y8=d* v8(1)/ze ze=rho- v9(2) : x9=-d* v9(0)/ze : y9=d* v9(1)/ze ze=rho-v10(2) : x10=-d*v10(0)/ze : y10=d*v10(1)/ze ze=rho-v11(2) : x11=-d*v11(0)/ze : y11=d*v11(1)/ze if (x1-x6)*(y1-y8)<(x1-x8)*(y1-y6) then ' face 0: 1, 6, 8 triangle x1+cenx,y1+ceny,x6+cenx,y6+ceny,x8+cenx,y8+ceny,&hFF0000,&hFF0000 endif if (x1-x8)*(y1-y0)<(x1-x0)*(y1-y8) then ' face 1: 1, 8, 0 triangle x1+cenx,y1+ceny,x8+cenx,y8+ceny,x0+cenx,y0+ceny,&h00FF00,&h00FF00 endif if (x1-x0)*(y1-y10)<(x1-x10)*(y1-y0) then ' face 2: 1, 0,10 triangle x1+cenx,y1+ceny,x0+cenx,y0+ceny,x10+cenx,y10+ceny,&h0000FF,&h0000FF endif if (x1-x10)*(y1-y7)<(x1-x7)*(y1-y10) then ' face 3: 1,10, 7 triangle x1+cenx,y1+ceny,x10+cenx,y10+ceny,x7+cenx,y7+ceny,&hFFFF00,&hFFFF00 endif if (x1-x7)*(y1-y6)<(x1-x6)*(y1-y7) then ' face 4: 1, 7, 6 triangle x1+cenx,y1+ceny,x7+cenx,y7+ceny,x6+cenx,y6+ceny,&hFF00FF,&hFF00FF endif if (x6-x7)*(y6-y3)<(x6-x3)*(y6-y7) then ' face 5: 6, 7, 3 triangle x6+cenx,y6+ceny,x7+cenx,y7+ceny,x3+cenx,y3+ceny,&h00FFFF,&h00FFFF endif if (x6-x3)*(y6-y9)<(x6-x9)*(y6-y3) then ' face 6: 6, 3, 9 triangle x6+cenx,y6+ceny,x3+cenx,y3+ceny,x9+cenx,y9+ceny,&hFF0000,&hFF0000 endif if (x6-x9)*(y6-y8)<(x6-x8)*(y6-y9) then ' face 7: 6, 9, 8 triangle x6+cenx,y6+ceny,x9+cenx,y9+ceny,x8+cenx,y8+ceny,&h00FF00,&h00FF00 endif if (x8-x9)*(y8-y4)<(x8-x4)*(y8-y9) then ' face 8: 8, 9, 4 triangle x8+cenx,y8+ceny,x9+cenx,y9+ceny,x4+cenx,y4+ceny,&h0000FF,&h0000FF endif if (x8-x4)*(y8-y0)<(x8-x0)*(y8-y4) then ' face 9: 8, 4, 0 triangle x8+cenx,y8+ceny,x4+cenx,y4+ceny,x0+cenx,y0+ceny,&hFFFF00,&hFFFF00 endif if (x0-x4)*(y0-y5)<(x0-x5)*(y0-y4) then ' face 10: 0, 4, 5 triangle x0+cenx,y0+ceny,x4+cenx,y4+ceny,x5+cenx,y5+ceny,&hFF00FF,&hFF00FF endif if (x0-x5)*(y0-y10)<(x0-x10)*(y0-y5) then ' face 11: 0, 5,10 triangle x0+cenx,y0+ceny,x5+cenx,y5+ceny,x10+cenx,y10+ceny,&h00FFFF,&h00FFFF endif if (x10-x5)*(y10-y11)<(x10-x11)*(y10-y5) then ' face 12: 10, 5,11 triangle x10+cenx,y10+ceny,x5+cenx,y5+ceny,x11+cenx,y11+ceny,&hFF0000,&hFF0000 endif if (x10-x11)*(y10-y7)<(x10-x7)*(y10-y11) then ' face 13: 10,11, 7 triangle x10+cenx,y10+ceny,x11+cenx,y11+ceny,x7+cenx,y7+ceny,&h00FF00,&h00FF00 endif if (x7-x11)*(y7-y3)<(x7-x3)*(y7-y11) then ' face 14: 7,11, 3 triangle x7+cenx,y7+ceny,x11+cenx,y11+ceny,x3+cenx,y3+ceny,&h0000FF,&h0000FF endif if (x3-x11)*(y3-y2)<(x3-x2)*(y3-y11) then ' face 15: 3,11, 2 triangle x3+cenx,y3+ceny,x11+cenx,y11+ceny,x2+cenx,y2+ceny,&hFFFF00,&hFFFF00 endif if (x2-x11)*(y2-y5)<(x2-x5)*(y2-y11) then ' face 16: 2,11, 5 triangle x2+cenx,y2+ceny,x11+cenx,y11+ceny,x5+cenx,y5+ceny,&hFF00FF,&hFF00FF endif if (x2-x5)*(y2-y4)<(x2-x4)*(y2-y5) then ' face 17: 2, 5, 4 triangle x2+cenx,y2+ceny,x5+cenx,y5+ceny,x4+cenx,y4+ceny,&h00FFFF,&h00FFFF endif if (x2-x4)*(y2-y9)<(x2-x9)*(y2-y4) then ' face 18: 2, 4, 9 triangle x2+cenx,y2+ceny,x4+cenx,y4+ceny,x9+cenx,y9+ceny,&hFFFFFF,&hFFFFFF endif if (x2-x9)*(y2-y3)<(x2-x3)*(y2-y9) then ' face 19: 2, 9, 3 triangle x2+cenx,y2+ceny,x3+cenx,y3+ceny,x9+cenx,y9+ceny,&h404040,&h404040 endif for iter = 1 to 720 cx = cos(2*iter) : sx = sin(2*iter) ' GRRR - rule change cy = cos(1*iter) : sy = sin(1*iter) ' must recalc rotation matrix cz = cos(.5*iter) : sz = sin(.5*iter) ' each iteration trot(0,0) = cz * cy trot(1,0) = sz * cy trot(2,0) = sy trot(0,1) = cz * sx * sy - sz * cx trot(1,1) = cz * cx + sz * sx * sy trot(2,1) = - sx * cy trot(0,2) = - cz * cx * sy - sz * sx trot(1,2) = cz * sx - sz * cx * sy trot(2,2) = cx * cy math v_mult trot(), v0(), vt0() ' rotate math v_mult trot(), v1(), vt1() ' 6 points math v_mult trot(), v2(), vt2() ' in math v_mult trot(), v3(), vt3() ' three math v_mult trot(), v4(), vt4() ' dimensions math v_mult trot(), v5(), vt5() math v_mult trot(), v6(), vt6() math v_mult trot(), v7(), vt7() math v_mult trot(), v8(), vt8() math v_mult trot(), v9(), vt9() math v_mult trot(),v10(),vt10() math v_mult trot(),v11(),vt11() bx = min(x0,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11)+cenx bh = max(x0,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11)+cenx+&h2 ' calculate by = min(y0,y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11)+ceny bv = max(y0,y1,y2,y3,y4,y5,y6,y7,y8,y9,y10,y11)+ceny+&h2 ' erasing box box bx,by,bh-bx,bv-by,,&h0,&h0 ' erase previous image - dynamic size calc ' box 193,92,416,420,0,0,0 ' slightly faster than calculated box ze=rho- vt0(2) : x0=-d* vt0(0)/ze : y0=d* vt0(1)/ze ' project 12 points ze=rho- vt1(2) : x1=-d* vt1(0)/ze : y1=d* vt1(1)/ze ze=rho- vt2(2) : x2=-d* vt2(0)/ze : y2=d* vt2(1)/ze ze=rho- vt3(2) : x3=-d* vt3(0)/ze : y3=d* vt3(1)/ze ze=rho- vt4(2) : x4=-d* vt4(0)/ze : y4=d* vt4(1)/ze ze=rho- vt5(2) : x5=-d* vt5(0)/ze : y5=d* vt5(1)/ze ze=rho- vt6(2) : x6=-d* vt6(0)/ze : y6=d* vt6(1)/ze ze=rho- vt7(2) : x7=-d* vt7(0)/ze : y7=d* vt7(1)/ze ze=rho- vt8(2) : x8=-d* vt8(0)/ze : y8=d* vt8(1)/ze ze=rho- vt9(2) : x9=-d* vt9(0)/ze : y9=d* vt9(1)/ze ze=rho-vt10(2) : x10=-d*vt10(0)/ze : y10=d*vt10(1)/ze ze=rho-vt11(2) : x11=-d*vt11(0)/ze : y11=d*vt11(1)/ze if (x1-x6)*(y1-y8)<(x1-x8)*(y1-y6) then ' face 0: 1, 6, 8 triangle x1+cenx,y1+ceny,x6+cenx,y6+ceny,x8+cenx,y8+ceny,&hFF0000,&hFF0000 endif if (x1-x8)*(y1-y0)<(x1-x0)*(y1-y8) then ' face 1: 1, 8, 0 triangle x1+cenx,y1+ceny,x8+cenx,y8+ceny,x0+cenx,y0+ceny,&h00FF00,&h00FF00 endif if (x1-x0)*(y1-y10)<(x1-x10)*(y1-y0) then ' face 2: 1, 0,10 triangle x1+cenx,y1+ceny,x0+cenx,y0+ceny,x10+cenx,y10+ceny,&h0000FF,&h0000FF endif if (x1-x10)*(y1-y7)<(x1-x7)*(y1-y10) then ' face 3: 1,10, 7 triangle x1+cenx,y1+ceny,x10+cenx,y10+ceny,x7+cenx,y7+ceny,&hFFFF00,&hFFFF00 endif if (x1-x7)*(y1-y6)<(x1-x6)*(y1-y7) then ' face 4: 1, 7, 6 triangle x1+cenx,y1+ceny,x7+cenx,y7+ceny,x6+cenx,y6+ceny,&hFF00FF,&hFF00FF endif if (x6-x7)*(y6-y3)<(x6-x3)*(y6-y7) then ' face 5: 6, 7, 3 triangle x6+cenx,y6+ceny,x7+cenx,y7+ceny,x3+cenx,y3+ceny,&h00FFFF,&h00FFFF endif if (x6-x3)*(y6-y9)<(x6-x9)*(y6-y3) then ' face 6: 6, 3, 9 triangle x6+cenx,y6+ceny,x3+cenx,y3+ceny,x9+cenx,y9+ceny,&hFF0000,&hFF0000 endif if (x6-x9)*(y6-y8)<(x6-x8)*(y6-y9) then ' face 7: 6, 9, 8 triangle x6+cenx,y6+ceny,x9+cenx,y9+ceny,x8+cenx,y8+ceny,&h00FF00,&h00FF00 endif if (x8-x9)*(y8-y4)<(x8-x4)*(y8-y9) then ' face 8: 8, 9, 4 triangle x8+cenx,y8+ceny,x9+cenx,y9+ceny,x4+cenx,y4+ceny,&h0000FF,&h0000FF endif if (x8-x4)*(y8-y0)<(x8-x0)*(y8-y4) then ' face 9: 8, 4, 0 triangle x8+cenx,y8+ceny,x4+cenx,y4+ceny,x0+cenx,y0+ceny,&hFFFF00,&hFFFF00 endif if (x0-x4)*(y0-y5)<(x0-x5)*(y0-y4) then ' face 10: 0, 4, 5 triangle x0+cenx,y0+ceny,x4+cenx,y4+ceny,x5+cenx,y5+ceny,&hFF00FF,&hFF00FF endif if (x0-x5)*(y0-y10)<(x0-x10)*(y0-y5) then ' face 11: 0, 5,10 triangle x0+cenx,y0+ceny,x5+cenx,y5+ceny,x10+cenx,y10+ceny,&h00FFFF,&h00FFFF endif if (x10-x5)*(y10-y11)<(x10-x11)*(y10-y5) then ' face 12: 10, 5,11 triangle x10+cenx,y10+ceny,x5+cenx,y5+ceny,x11+cenx,y11+ceny,&hFF0000,&hFF0000 endif if (x10-x11)*(y10-y7)<(x10-x7)*(y10-y11) then ' face 13: 10,11, 7 triangle x10+cenx,y10+ceny,x11+cenx,y11+ceny,x7+cenx,y7+ceny,&h00FF00,&h00FF00 endif if (x7-x11)*(y7-y3)<(x7-x3)*(y7-y11) then ' face 14: 7,11, 3 triangle x7+cenx,y7+ceny,x11+cenx,y11+ceny,x3+cenx,y3+ceny,&h0000FF,&h0000FF endif if (x3-x11)*(y3-y2)<(x3-x2)*(y3-y11) then ' face 15: 3,11, 2 triangle x3+cenx,y3+ceny,x11+cenx,y11+ceny,x2+cenx,y2+ceny,&hFFFF00,&hFFFF00 endif if (x2-x11)*(y2-y5)<(x2-x5)*(y2-y11) then ' face 16: 2,11, 5 triangle x2+cenx,y2+ceny,x11+cenx,y11+ceny,x5+cenx,y5+ceny,&hFF00FF,&hFF00FF endif if (x2-x5)*(y2-y4)<(x2-x4)*(y2-y5) then ' face 17: 2, 5, 4 triangle x2+cenx,y2+ceny,x5+cenx,y5+ceny,x4+cenx,y4+ceny,&h00FFFF,&h00FFFF endif if (x2-x4)*(y2-y9)<(x2-x9)*(y2-y4) then ' face 18: 2, 4, 9 triangle x2+cenx,y2+ceny,x4+cenx,y4+ceny,x9+cenx,y9+ceny,&hFFFFFF,&hFFFFFF endif if (x2-x9)*(y2-y3)<(x2-x3)*(y2-y9) then ' face 19: 2, 9, 3 triangle x2+cenx,y2+ceny,x3+cenx,y3+ceny,x9+cenx,y9+ceny,&h404040,&h404040 endif if iter = 650 then SaveVerts ' print @(700,0) iter : do : loop until inkey$ <> "" ' uncomment for step by step next iter print timer ShowVerts end sub SaveVerts vs0(0) = vt0(0) : vs0(1) = vt0(1) : vs0(2) = vt0(2) vs1(0) = vt1(0) : vs1(1) = vt1(1) : vs1(2) = vt1(2) vs2(0) = vt2(0) : vs2(1) = vt2(1) : vs2(2) = vt2(2) vs3(0) = vt3(0) : vs3(1) = vt3(1) : vs3(2) = vt3(2) vs4(0) = vt4(0) : vs4(1) = vt4(1) : vs4(2) = vt4(2) vs5(0) = vt5(0) : vs5(1) = vt5(1) : vs5(2) = vt5(2) vs6(0) = vt6(0) : vs6(1) = vt6(1) : vs6(2) = vt6(2) vs7(0) = vt7(0) : vs7(1) = vt7(1) : vs7(2) = vt7(2) vs8(0) = vt8(0) : vs8(1) = vt8(1) : vs8(2) = vt8(2) vs9(0) = vt9(0) : vs9(1) = vt9(1) : vs9(2) = vt9(2) vs10(0) = vt10(0) : vs10(1) = vt10(1) : vs10(2) = vt10(2) vs11(0) = vt11(0) : vs11(1) = vt11(1) : vs11(2) = vt11(2) end sub sub ShowVerts font 7 print : print "Vertex coordinates at iteration 650:" print vs0(0), vs0(1), vs0(2) print vs1(0), vs1(1), vs1(2) print vs2(0), vs2(1), vs2(2) print vs3(0), vs3(1), vs3(2) print vs4(0), vs4(1), vs4(2) print vs5(0), vs5(1), vs5(2) print vs6(0), vs6(1), vs6(2) print vs7(0), vs7(1), vs7(2) print vs8(0), vs8(1), vs8(2) print vs9(0), vs9(1), vs9(2) print vs10(0), vs10(1), vs10(2) print vs11(0), vs11(1), vs11(2) ' font 1 ' interesting font anomaly - screen scrolls up @ END if commented end sub icosashape: ' vertices 'data 12 data 0,132,213, 0,-132,213, 0,132,-213, 0,-132,-213 ' (0, 1, f) Where f = data 132,213,0, -132,213,0, 132,-213,0, -132,-213,0 ' (1, f, 0) (1 + v5) / 2 data 213,0,132, 213,0,-132, -213,0,132, -213,0,-132 ' ( f, 0, 1) golden ratio 1.618 ' faces 'data 20 data 1, 6, 8, 1, 8, 0, 1, 0,10, 1,10, 7 ' vertices for data 1, 7, 6, 6, 7, 3, 6, 3, 9, 6, 9, 8 ' each face in data 8, 9, 4, 8, 4, 0, 0, 4, 5, 0, 5,10 ' counter-clockwise data 10, 5,11, 10,11, 7, 7,11, 3, 3,11, 2 ' order data 2,11, 5, 2, 5, 4, 2, 4, 9, 2, 9, 3 Visit Vegipete's *Mite Library for cool programs. |
||||
| The Back Shed's forum code is written, and hosted, in Australia. | © JAQ Software 2026 |