
|

|
Forum Index : Microcontroller and PC projects : Snakes and Ladders Update
| Author | Message | ||||
| Nimue Guru Joined: 06/08/2020 Location: United KingdomPosts: 420 |
Hi I posted previously about using CMM2 / MMBasic to simulate Snakes and Ladders. As the game is totally deterministic with no skill, it's great to actually simulate. This has now become a GOTO (excuse the pun) activity in class that most students can create a working example after a couple of sessions learning MMBasic. Original post here... I use this board: 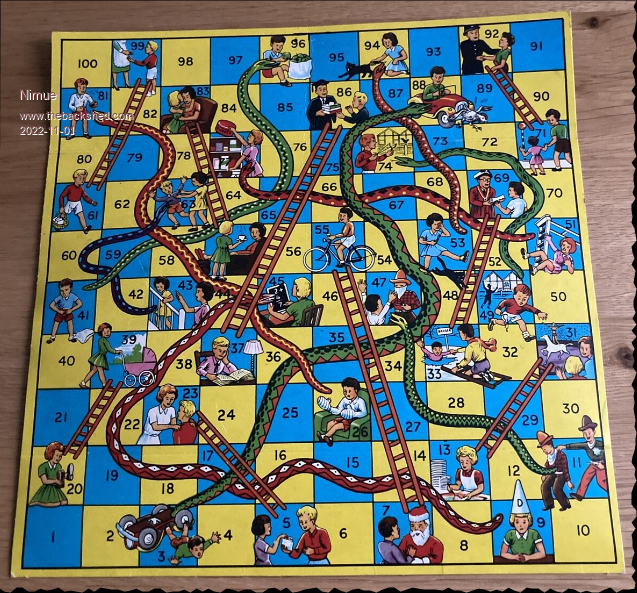 Recently a student offered this: option base 1 dim board(100) ' Snakes and Ladders simulation ' Pre populate board with squares that equal its number for x = 1 to 100 let board(x) = x next x ' load in structure of snakes and ladders from DATA statements for y = 1 to 18 read start, finish let board(start) = finish next y 'reset rolls and set number of simulations let roll_total = 0 let maxit = 10000 '10,000 gives a consistent overall average print "Simulating"maxit " individual games of Snakes and ladders." 'set up the simulation for runs = 1 to maxit let position = 1 let rolls = 0 do 'individual games roll = int((rnd*5)+0.5)+1 position = position + roll if position >= 100 then exit do position = board(position) rolls = rolls + 1 loop while position <100 roll_total = roll_total+rolls next runs print "Overall average after" maxit " rolls is" int((roll_total/maxit)+0.5) " rolls" 'ladders and then snakes data 5,23,7,55,13,31,20,39,33,69,37,86,57,83,61,99,71,92 data 45,9,47,11,63,43,74,49,77,51,81,26,88,3,94,53,96,41 I find it interesting that (a) many students have never played Snakes and Ladders and (b) As a kid myself, I never realised there was 0% input from the player other than to roll the dice. Entropy is not what it used to be |
||||
| Pilot352 Newbie Joined: 12/08/2020 Location: United StatesPosts: 34 |
Interesting project. I knew this game as "Shoots and Ladders" where the snakes in yours were slides (playground slides). I never knew there were different versions. |
||||
| Goksteroo Senior Member Joined: 15/03/2021 Location: AustraliaPosts: 114 |
Interesting.... We always played that you had to roll to the 100 square exactly and if you didn't the remainder of the dice count moved you away from the 100 square. 2 minor things though.... - They could have used Option Default Integer - good practice if only integers are used as there are some speed and memory advantages(although hardly needed in this case) - roll=int((rnd*5)+0.5)+1 introduces a bias and so imbalances the probabilities for the 1 and 6 dice. Try this code using their rnd routine and then the usually accepted roll=int(rnd*6)+1 and you'll see the difference in probabilities. dim num(6),num2(6) for x=1 to 100000 y=int((rnd*5)+0.5)+1 inc num(y) y=int(rnd*6)+1 inc num2(y) next t=0 t2=0 print "int((rnd*5)+0.5)+1) int(rnd6)+1" for x=1 to 6 print x;"-";num(x),,,,num2(x) t=t+num(x) t2=t2+num2(x) next x print t,,,,t2 |
||||
| Volhout Guru Joined: 05/03/2018 Location: NetherlandsPosts: 5089 |
My version, combines work from Nimue and Gokesteroo. With Volhout flavor.... Option base 1 Option default integer Dim board(100) 'the 100 squares of the board Dim bins(500) 'gather statistics of the runs (is zero'ed at creation) 'log what is rolled, just for curiousity Dim sequence(500) Dim shortest(100) ' Snakes and Ladders simulation ' Pre populate board with squares that equal its number For x = 1 To 100 board(x) = x Next x ' load in structure of snakes and ladders from DATA statements For y = 1 To 18 Read start, finish board(start) = finish Next y 'reset rolls and set number of simulations roll_total = 0 maxit = 10000 '10,000 gives a consistent overall average Print "Simulating" maxit " individual games of Snakes and ladders." 'statistics outside arrays max_rolls=0 min_rolls=1000 'run the 10000 simulations For runs = 1 To maxit position = 1 rolls = 0 Do 'individual games roll = Rnd*6 + 1 rolls = rolls + 1 sequence(rolls)=roll position = position + roll If position = 100 Then Exit If position > 100 Then position = 200 - position position = board(position) Loop 'max rolls remembered max_rolls = Max(max_rolls, rolls) 'min rolls shortest form 'min_rolls = Min(min_rolls, rolls) 'min rolls with memory of sequence rolled If rolls < min_rolls Then min_rolls=rolls 'copy sequence For i=1 To rolls shortest(i)=sequence(i) Next EndIf roll_total = roll_total + rolls bins(rolls)=bins(rolls) + 1 Next runs 'average Print "Average after" maxit " rolls is" roll_total/maxit " rolls" 'other valuable statistics qty = Math(max bins(),modal%) Print "modal rolls = " modal% " occurring ";qty;" times" Print "max rolls = " max_rolls Print "min rolls = " min_rolls 'the shortest path as remembered... Print "shortest path = "; For i=1 To min_rolls Print shortest(i), Next i 'ladders and then snakes Data 5,23,7,55,13,31,20,39,33,69,37,86,57,83,61,99,71,92 Data 45,9,47,11,63,43,74,49,77,51,81,26,88,3,94,53,96,41 > > outputs Saved 1846 bytes Simulating 10000 individual games of Snakes and ladders. Average after 10000 rolls is 57.4882 rolls modal rolls = 14 occurring 180 times max rolls = 452 min rolls = 3 shortest path = 6 6 1 Edited 2022-11-02 00:29 by Volhout PicomiteVGA PETSCII ROBOTS |
||||
| Nimue Guru Joined: 06/08/2020 Location: United KingdomPosts: 420 |
Nice - adding the shortest sequence. N Full version - with all feedback greatly received: ' Snakes and Ladders simulation ' Start off the board (position = 0) ' Only end when landing exactly on 100. If over roll, move back ' the surplus amount. So on 99, roll 4 (=103). Move forward 1 + ' (=100) then back 3. Final square = 97. cls option base 1 ' Board starts at square 1 option default integer 'variables integers by default dim board(100) dim bins(2000) dim sequence(2000) dim shortest(300) ' Pre populate board with squares that equal its number for x = 1 to 100 let board(x) = x next x ' load in structure of snakes and ladders for y = 1 to 13 read start,finish let board(start) = finish next y 'reset rolls and set number of simulations let roll_total = 0 let maxit = 10000 '10,000 gives a consistent overall average dim rolls(maxit) min_rolls=2000 print "Simulating"maxit " individual games of Snakes and ladders." 'set up the simulation for runs = 1 to maxit if runs mod 1000 = 0 then print @(10,30) runs let position = 0 ' start off the board let currnetroll = 0 do 'individual games currentroll = int((rnd*6))+1 position = position + currentroll rolls(runs) = rolls(runs) + 1 'keep count of number of rolls sequence(rolls(runs)) = currentroll if position = 100 then exit do if position > 100 then position = 100 - (position - 100) position = board(position) loop while position <100 bins(rolls(runs)) = bins(rolls(runs)) + 1 if rolls(runs) < min_rolls then min_rolls = rolls(runs) for i = 1 to rolls(runs) shortest(i)=sequence(i) next endif next runs roll_mean = int(math(mean rolls())) roll_median = math(median rolls()) roll_max = math(max rolls()) roll_min = math(min rolls()) max_freq = bins(roll_max) min_freq = bins(roll_min) median_freq = bins(roll_median) mean_freq = bins(roll_mean) modal_freq = math (max bins(), modal%) print"" print "Mode:",,, modal%, " (" modal_freq " times )" print "Mean:",,, roll_mean, " (" mean_freq " times )" print "Median:",, roll_median, " (" median_freq " times)" print "Max:",,, roll_max " (" max_freq " times)" print "Min:",,, roll_min, " (" min_freq " times)" print"" print "Shortest path ="; for i = 1 to min_rolls print shortest(i), next 'ladders and then snakes 'data 5,23,7,55,13,31,20,39,33,69,37,86,57,83,61,99,71,92 'data 45,9,47,11,63,43,74,49,77,51,81,26,88,3,94,53,96,41 'board 2 'data 5,17,13,31,21,37,28,64,48,52,54,91,62,98,76,86 'data 26,7,33,10,57,53,59,24,67,36,71,49,77,41,84,61,92,73,97,66 'board 3 'data 1,38,4,14,9,31,21,42,28,84,36,57,51,67,71,91,80,100 'data 16,5,47,26,49,11,56,53,62,19,64,60,87,17,93,74,95,75,98,78 'board 4 'data 4,20,12,26,22,61,29,48,33,43,56,87,65,84,86,100,94,97 'data 21,17,36,5,51,30,63,11,66,35,72,18,76,38,88,53,95,79,98,25 'board 5 'data 1,38,4,14,9,31,21,42,28,84,36,44,51,67,71,91,80,100 'data 16,6,47,26,49,11,56,53,62,19,64,60,87,24,93,73,95,75,98,78 'board 6 Star Wars data 8,25,21,82,43,77,50,91,54,93,62,96,66,87 data 46,5,48,11,83,19,92,53,95,24,98,28  Entropy is not what it used to be |
||||
| Volhout Guru Joined: 05/03/2018 Location: NetherlandsPosts: 5089 |
Statistics is a nice thing.... But sometimes not very logical. Your screendump is probably not from board #1. The sequence 6,6,1 is the shortest route on board #1. The probability of throwing 6,6,1 as first 3 rolls is 1/216. Therefore I would expect the shortest route (6,6,1) to be rolled 50 times (10000/216) And if unucky, maybe 20 times, or 10 times. But apparently your run of 10,000 did not have a singe 6,6,1 roll.... Even if you start OFF the board (square 0) the shortest route (4 length) is: 1,6,6,1 2,5,6,1 3,4,6,1 4,3,6,1 5 not, since you ladder up 6,1,6,1 This still have a probability of 1/259, so you would expect the shortest route to be present in 10,000 runs. Regards, Volhout PicomiteVGA PETSCII ROBOTS |
||||
| Goksteroo Senior Member Joined: 15/03/2021 Location: AustraliaPosts: 114 |
Stats all workout if you use the original board data statements and change the line 'for y = 1 to 13' to 'for y=1 to 18' to correctly read the snakes and ladders positions. Run the simulation over 1,000,000 times (yes, I have little to do these days!) gives me these results: Off board starting position gives minimum rolls of 4 in 3856 games - or 1:259 On board starting position gives minimum rolls of 3 in 4562 games - or 1:219 Both within acceptable tolerance as correctly calculated by Volhout. One curiosity - the longest game I saw had 788 rolls! That explains the poor kid who never seemed to win a game. Edited 2022-11-02 09:31 by Goksteroo |
||||
| Volhout Guru Joined: 05/03/2018 Location: NetherlandsPosts: 5089 |
Statistics say there is a possibility of infinity.... Probably not in 1,000,000 runs... PicomiteVGA PETSCII ROBOTS |
||||
| The Back Shed's forum code is written, and hosted, in Australia. | © JAQ Software 2025 |